Regressione logistica con Pytorch¶
In questo articolo voglio impementare un esempio di classificazione per mezzo di una regressione logistica, usando il pacchetto Pytorch per Python.
La spiegazione di cosa è una regressione logistica la lascio alla pagina di Wikipedia – Regressione Logistica, qui solo un estratto:
In statistica e in econometria, il modello logit, noto anche come modello logistico o regressione logistica, è un modello di regressione nonlineare utilizzato quando la variabile dipendente è di tipo dicotomico. L’obiettivo del modello è di stabilire la probabilità con cui un’osservazione può generare uno o l’altro valore della variabile dipendente; può inoltre essere utilizzato per classificare le osservazioni, in base alla caratteristiche di queste, in due categorie.
In parole povere:
Dati una serie di variabili indipendenti (o di ingresso) voglio predire una variabile di uscita, che può essere 1 o 0 (dicotomica). La variabile di uscita è anche chiamata label.
Il dataset che uso in questo esempio è preso dal corso di Edx – Introduction to Artificial Intelligence (AI)
Il dataset è costituito dalle informazioni mediche di 15000 paziente. Ogni riga corrisponde ad un paziente. Per ogni paziente ci sono una serie di dati medici, quali età, numero di gravidanze, glucosio, pressione, ed altro.
La label, quindi il dato che intendo predire con il mio modello, è costituito dall’essere il paziente diabetico o meno.
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import LabelBinarizer
Load dataset¶
Carico i dati dal foglio Excel
exc1 = pd.read_csv('diabetes.csv')
exc2 = pd.read_csv('doctors.csv', encoding = "ISO-8859-1")
Vediamo cosa contengono i due dataframe appena creati:
exc1.head()
exc2.head()
Preprocessing dei dati¶
I due dataframe exc1 e exc2 contengono tutti e due un PatientID, per cui devo concatenare i due dataframe orizzontalmente in base al PatientID.
Piccola parentesi su come fare il merge dei due dataframe
df1 = pd.DataFrame([['1','antonio'],['2','giuseppe']], columns=['numID','nome'])
df2 = pd.DataFrame([['1','verro'],['2','rossi'],['3','Bianchi']], columns=['numID','cognome'])
pd.merge(df1, df2, on='numID', how='outer')
Quindi la funzione merge() ha bisogno di due argomenti per fare il merge correttamente:
- on=’chiave per il merge’
- how=’outer’, viene usato un OR di tutte le chiavi, anche se uno dei due dataframe non ha il recordcon la chiave scelta
lista_pazienti = pd.merge(exc1, exc2, on='PatientID', how='outer')
lista_pazienti.head()
Vediamo un riassunto delle proprietà statistiche del dataframe.
lista_pazienti.describe()
Salta subito all’occhio che la funzione ha fatto la statistica anche di PatientID, che è un codice numerico rappresentante il paziente pertanto deve essere considerato come una stringa piuttosto che un numero.
Cambio il tipo dei dati con la funzione astype()
lista_pazienti['PatientID'] = lista_pazienti['PatientID'].astype(str)
Vediamo quali sono le colonne aventi dati numerici, usiamo la funzione select_dtypes(). Verifichiamo che PatientID non è tra questi.
lista_pazienti.select_dtypes(include='number').head()
Ci sono elementi non definiti (nan) nelle righe? Possiamo usare la funzione count.
lista_pazienti.count()
Il dataframe ha 15000 righe ed ogni campo(o colonna) ha 15000 elementi. Quindi apparentemente non ci sono nan. Dico apparentemente perché potrebbero essere stati definiti con una codifica particolare, per esempio usando un numero molto negativo (-999) per l’indice di massa corporea (BMI), quando questo può essee un valore solo positivo.
Per riconoscere questi casi particolari dovremmo esplorare visualmente il dataframe e in caso scrivere un codice ad hoc.
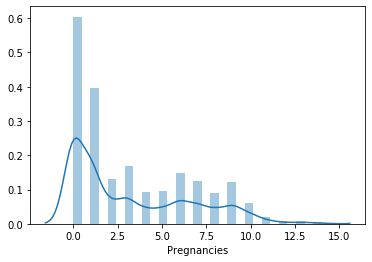
Vediamo la distribuzione dei valori per ogni colonna. Per questo userò la funzione distplot() del pacchetto seaborn.
sns.distplot(lista_pazienti.Pregnancies)
plt.show()
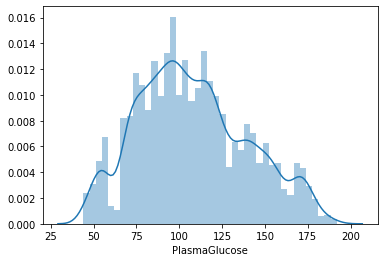
sns.distplot(lista_pazienti.PlasmaGlucose)
plt.show()
sns.distplot(lista_pazienti.DiastolicBloodPressure)
plt.show()
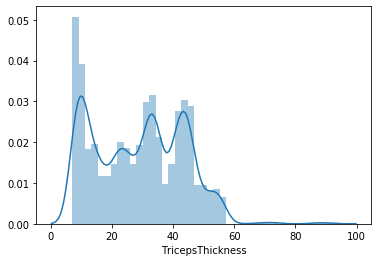
sns.distplot(lista_pazienti.TricepsThickness)
plt.show()
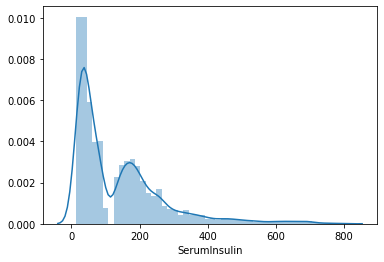
sns.distplot(lista_pazienti.SerumInsulin)
plt.show()
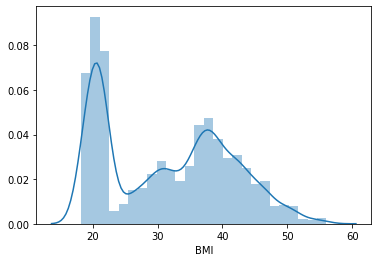
sns.distplot(lista_pazienti.BMI)
plt.show()
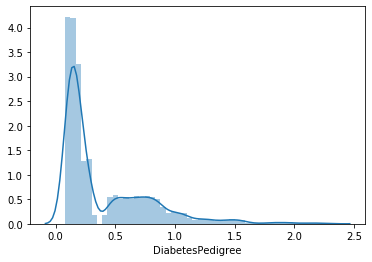
sns.distplot(lista_pazienti.DiabetesPedigree)
plt.show()
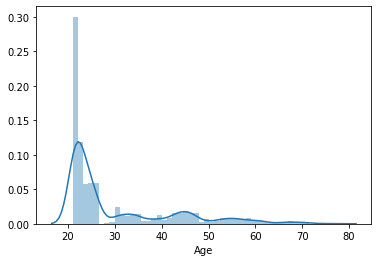
sns.distplot(lista_pazienti.Age)
plt.show()
Poiché il campo dell’età (Age) è piuttosto sbilanciato, il tutorial di Edx suggeriva di usare log(Age) al suo posto.
Aggiungiamo una colonna con log(Age):
lista_pazienti['logAge'] = np.log10(lista_pazienti['Age'].values)
sns.distplot(lista_pazienti.logAge)
plt.show()
Adesso voglio normalizzare i dati perché la convergenza è più facile quando i dati sono normalizzati.
La normalizzazione avviene per colonna. Per le colonne che hanno una distribuzione simile a quella gaussiana (o normale), posso normalizzare usando lo Z-score, ovvero si calcola la media ($\mu$) e la varianza ($\sigma^2$) dei dati in una colonna e poi si normalizza ogni singolo elemento della colonna secondo:
\begin{equation*}
\hat{x_i} = \frac{(x_i – \mu)}{\sigma^2} \quad \forall i
\end{equation*}
Per le colonne che non hanno una distribuzione simil-gaussiana posso usare una normalizzazione max-min. Ovvero calcolo il max dei dai su una colonna ($M$) e il minimo ($m$) degli stessi. Dopodichè applico la normalizzazione:
\begin{equation*}
\hat{x_i} = \frac{(x_i – m)}{(M-m)} \quad \forall{i}
\end{equation*}
Per fortuna non dobbiamo farlo manualmente, ma possiamo usare le funzioni di scikit-learn StandardScaler() e MinMaxScaler().
from sklearn.preprocessing import StandardScaler, MinMaxScaler
Prima di lavorare sul mio dataset faccio un esempio di uso di MinMaxScaler():
Mmsc = MinMaxScaler()
preg_norm = Mmsc.fit_transform(lista_pazienti.Pregnancies.values.astype(np.float64).reshape(-1,1))
print(preg_norm.max())
print(preg_norm.min())
In questo caso ho usato la funzione fit_transform()
Definisco su quali colonne usare l’algoritmo MinMax e su quali il Zscore:
columns_minmax = ['Pregnancies','SerumInsulin','BMI','DiabetesPedigree','logAge']
columns_zscore = ['PlasmaGlucose','DiastolicBloodPressure','TricepsThickness']
lista_pazienti_norm = pd.DataFrame(index=range(15000))
for column in columns_minmax:
lista_pazienti_norm[column + '_norm'] = Mmsc.fit_transform(lista_pazienti[column].values.astype(np.float64).reshape(-1, 1))
for column in columns_zscore:
lista_pazienti_norm[column + '_norm'] = Mmsc.fit_transform(lista_pazienti[column].values.astype(np.float64).reshape(-1, 1))
lista_pazienti_norm[lista_pazienti.select_dtypes(exclude='number').columns] = lista_pazienti.select_dtypes(exclude='number') #colonne non mumeriche
lista_pazienti_norm['Diabetic'] = lista_pazienti['Diabetic'] #È la label del modello
lista_pazienti_norm.head()
Un’ultima considerazione. Il valore di PatientID probabilmente non influisce sul risultato. Cioè non dovrebbe esserci alcuna correlazione tr il PatientID e la label (Diabetic).
Invece potrebbe esserci correlazione tra il medico (Physician) e il fatto che il paziente sia diabetico. Un cattivo medico aumenta la probabilità che il paziente si ammali. Per cui decido di usare l’informazione sul nome del medico.
Come primo passo voglio vedere quanti sono i medici nella lista. Utilizzo la funzione unique() per vedere quali sono i valori unici della colonna Physician. E shape per contarli.
lista_pazienti_norm.Physician.unique().shape
In tutto ho 109 medici. 109 medici su 15000 dati… può essere che ci sia una correlazione.
La regressione logistica è un algoritmo puramente matematico, che fa uso di numeri per determinare una uscita. Se voglio usare la colonna Physician, devo trasformare i valori in una informazione numerica che possa essere usata dall’algoritmo.
Per fare questo uso il one-hot-encoding. Scikit-learn ha una funzione apposta per realizzare l’encoding, si chiama LabelBinarizer()
lb = LabelBinarizer()
Phis_ohe = lb.fit_transform(lista_pazienti_norm.Physician)
Phis_ohe.shape
L’output di LabelBinarizer() è un array bidimensionale. Per comodità voglio mettere tutti i dati in un dataframe, per cui devo dare un nome a ciscuna delle colonne di Phis_ohe.
columns_name = []
for i in range(109):
columns_name += ['phis_ohe' + str(i)]
Creo il dataframe con i dati Phis_ohe e i nomi delle colonne columns_name
lista_dottori = pd.DataFrame(Phis_ohe, columns=columns_name)
Concateno la lista dei pazienti e quella dei dottori, poichè l’ordine delle righe non è cambiato, posso semplicemente accostarle una con l’altra (axis=1):
lista_pazienti_e_dottori = pd.concat([lista_pazienti_norm, lista_dottori], axis=1)
Dal dataframe devo rimuovere alcune colonne
#rimuovo la colonna Physician che è stata rimpiazzata dalla stessa informazione codificata
#rimuovo la colonna PatientID perché non è informativa
#rimuovo la colonna Diabetic perché costituisce il dato da predire
lista_pazienti_e_dottori = lista_pazienti_e_dottori.drop(columns=['Physician','PatientID','Diabetic'])
lista_pazienti_e_dottori.head()
lista_pazienti_e_dottori.shape
In realtà, rimane aperta una questione. Come trattare i pazienti che hanno più di una riga? Probabilmente si tratta di pazienti che hanno registrato dati in momenti diversi, in due viste diverse. Al momento decido di non riservare a questi pazienti un particolare trattamento, cioè li tratto come se fossero due pazienti diversi con dati diversi. In effetti dando un’occhiata veloce, lo stesso paziente può avere dati molto diversi tra loro.
Questi sono i pazienti duplicati:
lista_pazienti.loc[lista_pazienti.PatientID.duplicated(),:].head()
Partizionare il dataset¶
Divido i dati di ingresso in un set per il training e un set per il test.
Per farlo utilizzo la funzione train_test_split() di scikit-learn
from sklearn.model_selection import train_test_split
input_data = lista_pazienti_e_dottori.values.astype(np.float32) #le operazioni con i tensori richiedono il tipo float
label_data = lista_pazienti.Diabetic.values.astype(np.float32)
input_data_train, input_data_test, label_train, label_test = train_test_split(input_data, label_data, test_size=0.3)
Converto i numpy array in tensori:
input_data_train_tens = torch.from_numpy(input_data_train)
input_data_test_tens = torch.from_numpy(input_data_test)
label_train_tens = torch.from_numpy(label_train).view(-1,1)
label_test_tens = torch.from_numpy(label_test).view(-1,1)
Si noti che avrei anche potuto convertire in float in questo punto, con:
label_train_tens = torch.from_numpy(label_train).type(dtype=torch.float).view(-1,1) label_test_tens = torch.from_numpy(label_test).type(dtype=torch.float).view(-1,1)
Definizione del modello¶
Definiamo un modello costituito dalla sequenza di un layer lineare e dalla funzione Sigmoid().
Questo realizza il semplice modello della regressione logistica, definito come segue:
\begin{equation}
h(\bar x) = \sigma (\bar w \cdot \bar x+b)
\end{equation}
dove:
- $\bar x$ è l’ingresso pluridimensionale Nx1
- $\bar{w}$ è il vettore 1xN contenente il peso di ciascun ingresso
- $b$ è uno scalare
- $\sigma$ è la funzione Sigmoid(), che è una funzione da $\mathbb{R}$ in $\Bbb{R}$ definita come segue:
\begin{equation}
\sigma(z) = \frac{1}{1 + e^{-z}}
\end{equation}
- $h(\bar x)$ è l’uscita del modello, ed esprime la probabilità che che l’uscita sia 1
Per implementare questo modello utilizziamo un modello Sequential(), composto da un layer lineare e un layer che implementa la funzione sigmoid.
Il modello avrà 117 ingressi (tante sono le variabili di ingresso di lista_pazienti_e_dottori) e 1 uscita:
model_logreg = nn.Sequential(
nn.Linear(117,1),
nn.Sigmoid()
)
list(model_logreg.parameters())
Verifichiamo che funzioni, generando una uscita scalare:
output_data_train = model_logreg( input_data_train_tens )
output_data_train.shape
Definiamo come funzione errore la funzione Binary Cross Entropy BCELoss(), questa è cosi definita:
\begin{equation}
error(x) = \sum_{k=1}^n \left[ -y \cdot log(h(x)) – (1-y) \cdot log(1-h(x)) \right]
\end{equation}
dove:
$y$ è la label, cioè il valore vero
$h(x)$ è l’uscita del modello di regressione, compreso tra 0 e 1, esprime la probabilità che l’uscita sia 1.
error = nn.BCELoss()
Definisco un ottimizzatore, precisamente lo stochastic gradient descent SGD, con argomenti i parametri del modello di regressione logistico e il learning rate:
learning_rate = 1
optimizer = torch.optim.SGD(model_logreg.parameters(), lr = learning_rate)
In loop eseguiamo i seguenti step:
- calcolo dell’uscita con i parametri correnti
- calcolo dell’errore
- calcolo del gradiente
- aggiornamento dei parametri
- azzeramneto del gradiente
for i in range(1000):
output_data_train = model_logreg( input_data_train_tens ) #calcolo l'uscita
loss = error(output_data_train, label_train_tens) #calcolo l'errore
loss.backward() #calcolo del gradiente
optimizer.step() #aggiornamento dei parametri
optimizer.zero_grad() #azzeramento del gradiente
if np.mod(i,100)==0:
print(loss)
output_data_test = model_logreg( torch.from_numpy(input_data_test) )
loss = error(output_data_test, label_test_tens)
loss
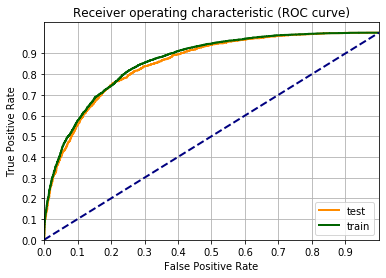
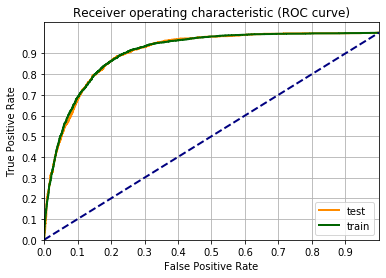
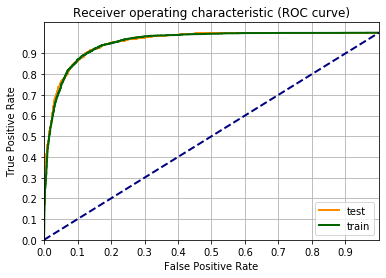
Una metrica per definire la bontà del modello è la curva ROC.
Un’occhiata alla pagina di Wikipedia vi chiarirà tutto sulla curva ROC.
Facciamo il grafico della curva ROC, usando la funzione roc_curve() di scikit-learn. Il codice sotto è un adattamento dell’esempio sulla pagina di scikit-learn Receiver Operating Characteristic (ROC).
from sklearn.metrics import roc_curve
fpr_train, tpr_train, _ = roc_curve(label_train_tens,output_data_train.detach())
fpr_test, tpr_test, _ = roc_curve(label_test_tens ,output_data_test.detach())
fgr1 = plt.figure()
lw = 2
plt.plot(fpr_test, tpr_test, color='darkorange', label="test", lw=lw)
plt.plot(fpr_train, tpr_train, color='darkgreen', label="train", lw=lw)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1])
plt.ylim([0.0, 1.05])
plt.xticks(np.arange(0, 1, 0.1))
plt.yticks(np.arange(0, 1, 0.1))
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic (ROC curve)')
plt.legend(loc="lower right")
plt.grid(which='both')
plt.show()
Una metrica più semplice è la confusion matrix. Che può essere spiegata con il grafico sotto.
Come si vede ho due assi, valore vero e valore predetto.
Ogni esempio del dataset può essere inserito in una delle quattro classi:
- true positive (tp): il valore vero è 1 e il valore predetto è 1
- false positive (fp): il valore vero è 0 ma il valore predetto è 1
- true negative (tn): il valore vero è 0 e il valore predetto è 0
- false negative (fn): il valore vero è 1 ma il valore predetto è 0
Come si intuisce due delle classi sono correttamente classificate (true positive e true negative), mentre le altre due sono classificate erroneamente.
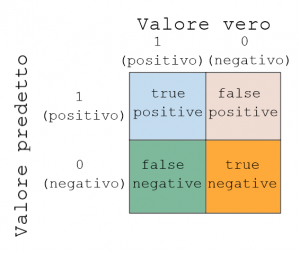
Scikit-learn ci mette a disposizione la funzione confusion_matrix() per fare questo calcolo:
from sklearn.metrics import confusion_matrix
output_data_train = model_logreg( input_data_train_tens )
output_data_train = (output_data_train.detach()>0.5).numpy()
tn, fp, fn, tp = confusion_matrix(label_train, output_data_train ).ravel()
tn, fp, fn, tp
Con questi valori posso costruire altre metriche:
$
Accuratezza: \quad A = \frac{\text{nr. di esempi correttamente classificati}}{\text{nr. totale di esempi}} = \frac{tp+tn}{tp+tn+fn+fp}
$
$
Precisione: \quad P = \frac{\text{nr. di true positive}}{\text{nr. di predizioni positive}} = \frac{tp}{tp+fp}
$
$
Recall: \quad R = \frac{\text{nr. di true positive}}{\text{nr. veri positivi}} = \frac{tp}{tp+fn}
$
$
F_1 score: \quad F_1 = 2 \frac{P\cdot R}{P+R}
$
A = (tp+tn)/(tp+tn+fn+fp)
P = tp/(tp+fp)
R = tp/(tp+fn)
F1 = 2*(P*R)/(P+R)
print('L\'accuratezza è %0.1f%%' %(A*100))
print('La precisione è %0.1f%%' %(P*100))
print('Il recall è %0.1f%%' %(R*100))
print('Il punteggio F1 è %0.1f%%' %(F1*100))
Un punteggio F1 non molto al di sopra del 50% (probabilità di indovinare il lato di una moneta bilanciata) non è un gran punteggio. Vediamo se riesco a tirarne fuori qualcosa di più.
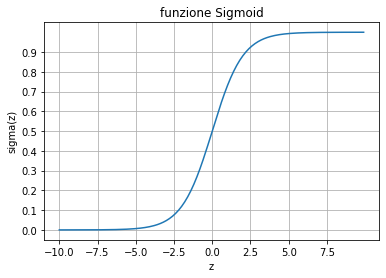
Ricordiamo come funziona la regressione logistica. Per semplificare consideriamo il caso di due ingressi $x1$ e $x2$.
Gli ingressi sono combinati linearnemente con i pesi $w1$ e $w2$, un fattore bias $b$ viene sommato: $z=w_1 \cdot x_1 + w_2 \cdot x_2 + b$
La somma viene applicata alla funzione sigmoid $\sigma(z)$, la cui uscita è compresa tra 0 e 1.
Sul risultato della funzione sigmoid viene fatta la decisione:
\begin{equation}
\sigma(z) > 0.5 \implies y=1
\end{equation}
\begin{equation}
\sigma(z) \le 0.5 \implies y=0
\end{equation}
x = np.arange(-10,10,0.1)
x_tens = torch.from_numpy(x)
y = torch.sigmoid( x_tens )
plt.plot( x,y.numpy() )
plt.xticks(np.arange(-10, 10, 2.5))
plt.yticks(np.arange(0, 1, 0.1))
plt.grid(which='both')
plt.xlabel('z')
plt.ylabel('sigma(z)')
plt.title('funzione Sigmoid')
plt.show()
Come si vede dal grafico della funzione Sigmoid sopra, $\sigma(z)$ è maggiore di 0.5 se z > 0. Ovvero se:
\begin{equation}
w_1 \cdot x_1 + w_2 \cdot x_2 + b > 0
\end{equation}
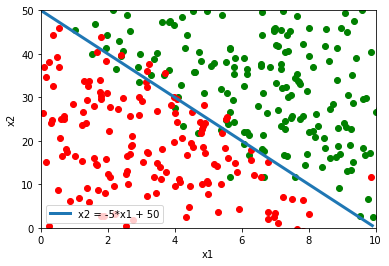
La disequazione sopra definisce una regione dello spazio bidimensionale delimitata dalla retta:
$x_2 = -\frac{w_1}{w_2} x_1 – \frac{b}{w_2}$
Questa divisione dello spazio può andare bene in alcuni casi casi, per esempio nella situazione sotto la retta riesce a classificare abbastanza bene tra punti verdi e punti rossi.
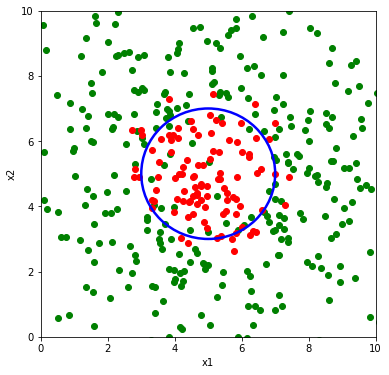
Invece nel caso rappresentato sotto, una retta non darebbe buoni risultati nella classificazione tra punti rossi e verdi. Serve invece qualcosa come una circonferenza. Ovvero qualcosa del tipo:
\begin{equation}
(x_1-x_{1,0})^2 + (x_2-x_{2,0})^2 = R^2
\end{equation}
Quindi occorre che nel modello di regressione compaiano anche i termini al quadrato degli ingressi $x_1$ e $x_2$.
Questa tecnica si chiama features mapping, e consiste nel definire (mappare) come nuove features di ingresso le potenze degli ingressi originali e tutti i possibili prodotti. Per esempio, nel caso sotto potrei considerare come features di ingresso i seguenti:
\begin{equation}
input =
\begin{bmatrix}
x_1\cr
x_2\cr
x_1\cdot x_2\cr
x_1^2\cr
x_2^2
\end{bmatrix}
\end{equation}
Una volta introdotti i termini quadratici tra gli ingressi, l’ottimizzatore riuscirà (speriamo) a trovare la giusta combinazione di questi per ottenere il contorno di decisione di forma circolare come nella figura sottostante.
La cosa che potrebbe non essere immediatamente chiara adesso è: cosa vuol dire aggiungere i termini non lineari agli ingressi?
Basta guardare la figura sotto per rendersene conto. Devo aggiungere al np.array() originario le colonne con i termini non lineari.
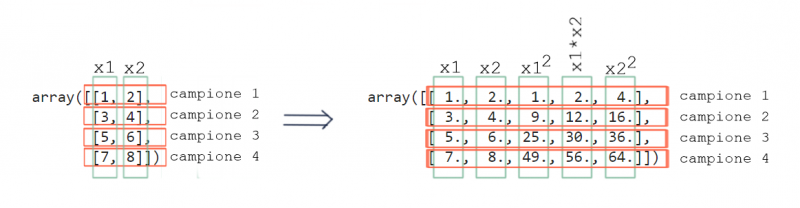
Ovviamente una volta appresa la tecnica del features mapping possiamo sbizzarrirci ad aggiungere potenze di qualsiasi ordine. In questo modo il contorno che definisce la soglia di decisione prenderà le forme più disparate (attenzione all’overfitting!). Facciamo ancora un esempio con le potenze al cubo.
In questo caso gli ingressi saranno:
\begin{equation}
input =
\begin{bmatrix}
x_1\cr
x_2\cr
x_1\cdot x_2\cr
x_1^2\cr
x_2^2\cr
x_1^2\cdot x_2\cr
x_1\cdot x_2^2\cr
x_1^3\cr
x_2^3
\end{bmatrix}
\end{equation}
Per generare i termini non lineari di un numpy array x (ogni colonna una feature diversa) uso il codice sotto. La programmazione di questo mi ha dato abbastanza mal di testa, usatelo con cautela.
def generateNonLinearFeatures(x,max_exp):
#given a marix with features in column, generate a new matrix with all the polynomial combination up to max_exp
import itertools
terms = []
num_feat = x.shape[1]
#il prossimo comando genera una lista delle possibili combinazioni delle variabili fino al max_exp
#Esempio: num_Feat=2 max_exp=2 genera:
#[(0, 0), (0, 1), (0, 2), (1, 1), (1, 2), (2, 2)] corrispondenti a:
# x^0 x^0 x^0 x^1 x^0 x^2 x^1 x^1 x^1 x^2 x^2 x^2
terms = list(itertools.combinations_with_replacement(list(range(num_feat+1)), max_exp))
if 'pol' in locals(): #rimuove la variabile pol se esiste già
del pol
for i in range(len(terms)):
polcol = np.ones(x.shape[0]).reshape(x.shape[0],1)
sum=0
for j in range(max_exp):
# print(i,j) #for debug only
sum=sum+int(terms[i][j])
if terms[i][j]!=0:
polcol = np.multiply(polcol,x[:,int(terms[i][j])-1].reshape(x.shape[0],1))
if (sum!=0): #exclude case all zeros (0,0), don't add the column
if 'pol' in locals():
pol = np.column_stack([pol, polcol])
else:
pol = polcol
return pol
Per generare le features non lineari decido di rinunciare alla codifica dei dottori perché sono 109 colonne che renderebbero il calcolo molto pesante. Potrei concatenare la lista alla fine senza termini non lineari. Per il momento la lascio fuori.
Riparto dal dataframe dei pazienti, normalizzato:
lista_pazienti_norm2 = lista_pazienti_norm.drop(columns=['Diabetic','Physician','PatientID'])
# lista_pazienti_norm2.values
Genero i termini non lineari fino al secondo ordine, si noti che la funzione generateNonLinearFeatures necessita come argomento un array (non un dataframe) per cui devo usare l’attributo .values
lista_pazient_norm_nl = generateNonLinearFeatures(lista_pazienti_norm2.values,2)
Ridefinisco la label e verifico che la lunghezza dei vettori sia corretta
label = lista_pazienti_norm.Diabetic.values
lista_pazient_norm_nl.shape, label.shape
Divido il dataset in test e train:
lista_pazienti_norm_nl_train, lista_pazienti_norm_nl_test, label_train, label_test = train_test_split(lista_pazient_norm_nl, label, test_size=0.3)
lista_pazienti_norm_nl_train.shape, lista_pazienti_norm_nl_test.shape, label_train.shape, label_test.shape
Converto gli array in tensori con elementi float:
input_data_train_tens = torch.from_numpy(lista_pazienti_norm_nl_train).type(dtype=torch.float)
input_data_test_tens = torch.from_numpy(lista_pazienti_norm_nl_test).type(dtype=torch.float)
label_train_tens = torch.from_numpy(label_train).type(dtype=torch.float).view(-1,1)
label_test_tens = torch.from_numpy(label_test).type(dtype=torch.float).view(-1,1)
Sono un po’ paranoico con le verifiche:
input_data_train_tens.shape, label_train_tens.shape
Ridefinisco il modello sequenziale con il giusto numero di ingressi:
model_logreg = nn.Sequential(
nn.Linear(input_data_train_tens.shape[1],1),
nn.Sigmoid()
)
definisco l’ottimizzatore
learning_rate = 0.1
optimizer = torch.optim.Adam(model_logreg.parameters(), lr = learning_rate)
e il loop di training del modello
for i in range(1000):
output_data_train = model_logreg( input_data_train_tens ) #calcolo l'uscita
loss = error(output_data_train, label_train_tens) #calcolo l'errore
loss.backward() #calcolo del gradiente
optimizer.step() #aggiornamento dei parametri
optimizer.zero_grad() #azzeramento del gradiente
if np.mod(i,100)==0:
print(loss)
calcolo l’uscita per il dataset si test, per il dataset di train ce l’ho già dal loop precedente:
output_data_test = model_logreg( input_data_test_tens )
Calcolo e grafico le curve ROC
fpr_train, tpr_train, _ = roc_curve(label_train_tens,output_data_train.detach())
fpr_test, tpr_test, _ = roc_curve(label_test_tens ,output_data_test.detach())
fgr1 = plt.figure()
lw = 2
plt.plot(fpr_test, tpr_test, color='darkorange', label="test", lw=lw)
plt.plot(fpr_train, tpr_train, color='darkgreen', label="train", lw=lw)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1])
plt.ylim([0.0, 1.05])
plt.xticks(np.arange(0, 1, 0.1))
plt.yticks(np.arange(0, 1, 0.1))
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic (ROC curve)')
plt.legend(loc="lower right")
plt.grid(which='both')
plt.show()
Applico la funzione di decisione della classe:
# output_data_train = model_logreg( input_data_train_tens )
# output_data_train_bin = (output_data_train.detach()>0.5).numpy()
output_data_test_bin = (output_data_test.detach()>0.5).numpy()
calcolo la matrice di confusione:
tn, fp, fn, tp = confusion_matrix(label_test_tens, output_data_test_bin ).ravel()
e le quantità ad essa connesse:
A = (tp+tn)/(tp+tn+fn+fp)
P = tp/(tp+fp)
R = tp/(tp+fn)
F1 = 2*(P*R)/(P+R)
print('L\'accuratezza è %0.1f%%' %(A*100))
print('La precisione è %0.1f%%' %(P*100))
print('Il recall è %0.1f%%' %(R*100))
print('Il punteggio F1 è %0.1f%%' %(F1*100))
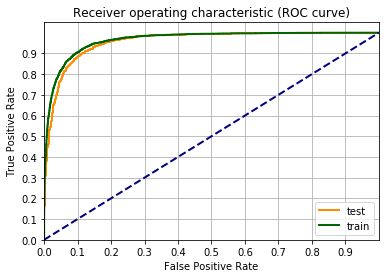
Quindi aggiungendo i termini quadratici il punteggio F1 è salito dal 66% al 73%.
Proviamo ad aggiungere i termini al cubo. Ovviamente una cosa intelligente sarebbe quella di raccogliere tutti gli step in una funzione. Cosa che non farò, affidandomi al più veloce CUT and PASTE di Jupyter.
lista_pazient_norm_nl = generateNonLinearFeatures(lista_pazienti_norm2.values,3)
label = lista_pazienti_norm.Diabetic.values
lista_pazienti_norm_nl_train, lista_pazienti_norm_nl_test, label_train, label_test = train_test_split(lista_pazient_norm_nl, label, test_size=0.3)
input_data_train_tens = torch.from_numpy(lista_pazienti_norm_nl_train).type(dtype=torch.float)
input_data_test_tens = torch.from_numpy(lista_pazienti_norm_nl_test).type(dtype=torch.float)
label_train_tens = torch.from_numpy(label_train).type(dtype=torch.float).view(-1,1)
label_test_tens = torch.from_numpy(label_test).type(dtype=torch.float).view(-1,1)
model_logreg = nn.Sequential(
nn.Linear(input_data_train_tens.shape[1],1),
nn.Sigmoid()
)
learning_rate = 0.1
optimizer = torch.optim.Adam(model_logreg.parameters(), lr = learning_rate)
for i in range(1000):
output_data_train = model_logreg( input_data_train_tens ) #calcolo l'uscita
loss = error(output_data_train, label_train_tens) #calcolo l'errore
loss.backward() #calcolo del gradiente
optimizer.step() #aggiornamento ei parametri
optimizer.zero_grad() #azzeramento del gradiente
if np.mod(i,100)==0:
print(loss)
output_data_test = model_logreg( input_data_test_tens )
fpr_train, tpr_train, _ = roc_curve(label_train_tens,output_data_train.detach())
fpr_test, tpr_test, _ = roc_curve(label_test_tens ,output_data_test.detach())
fgr1 = plt.figure()
lw = 2
plt.plot(fpr_test, tpr_test, color='darkorange', label="test", lw=lw)
plt.plot(fpr_train, tpr_train, color='darkgreen', label="train", lw=lw)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1])
plt.ylim([0.0, 1.05])
plt.xticks(np.arange(0, 1, 0.1))
plt.yticks(np.arange(0, 1, 0.1))
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic (ROC curve)')
plt.legend(loc="lower right")
plt.grid(which='both')
plt.show()
# output_data_train = model_logreg( input_data_train_tens )
# output_data_train_bin = (output_data_train.detach()>0.5).numpy()
output_data_test_bin = (output_data_test.detach()>0.5).numpy()
tn, fp, fn, tp = confusion_matrix(label_test_tens, output_data_test_bin ).ravel()
A = (tp+tn)/(tp+tn+fn+fp)
P = tp/(tp+fp)
R = tp/(tp+fn)
F1 = 2*(P*R)/(P+R)
print('L\'accuratezza è %0.1f%%' %(A*100))
print('La precisione è %0.1f%%' %(P*100))
print('Il recall è %0.1f%%' %(R*100))
print('Il punteggio F1 è %0.1f%%' %(F1*100))
Sembra che il gioco funzioni piuttosto bene, sono passato da un F1 di 73% ad uno di 83%. Vediamo fino a dove posso spingermi.
lista_pazient_norm_nl = generateNonLinearFeatures(lista_pazienti_norm2.values,4)
label = lista_pazienti_norm.Diabetic.values
lista_pazienti_norm_nl_train, lista_pazienti_norm_nl_test, label_train, label_test = train_test_split(lista_pazient_norm_nl, label, test_size=0.3)
input_data_train_tens = torch.from_numpy(lista_pazienti_norm_nl_train).type(dtype=torch.float)
input_data_test_tens = torch.from_numpy(lista_pazienti_norm_nl_test).type(dtype=torch.float)
label_train_tens = torch.from_numpy(label_train).type(dtype=torch.float).view(-1,1)
label_test_tens = torch.from_numpy(label_test).type(dtype=torch.float).view(-1,1)
model_logreg = nn.Sequential(
nn.Linear(input_data_train_tens.shape[1],1),
nn.Sigmoid()
)
learning_rate = 0.1
optimizer = torch.optim.Adam(model_logreg.parameters(), lr = learning_rate)
for i in range(1000):
output_data_train = model_logreg( input_data_train_tens ) #calcolo l'uscita
loss = error(output_data_train, label_train_tens) #calcolo l'errore
loss.backward() #calcolo del gradiente
optimizer.step() #aggiornamento ei parametri
optimizer.zero_grad() #azzeramento del gradiente
if np.mod(i,100)==0:
print(loss)
output_data_test = model_logreg( input_data_test_tens )
fpr_train, tpr_train, _ = roc_curve(label_train_tens,output_data_train.detach())
fpr_test, tpr_test, _ = roc_curve(label_test_tens ,output_data_test.detach())
fgr1 = plt.figure()
lw = 2
plt.plot(fpr_test, tpr_test, color='darkorange', label="test", lw=lw)
plt.plot(fpr_train, tpr_train, color='darkgreen', label="train", lw=lw)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1])
plt.ylim([0.0, 1.05])
plt.xticks(np.arange(0, 1, 0.1))
plt.yticks(np.arange(0, 1, 0.1))
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic (ROC curve)')
plt.legend(loc="lower right")
plt.grid(which='both')
plt.show()
# output_data_train = model_logreg( input_data_train_tens )
# output_data_train_bin = (output_data_train.detach()>0.5).numpy()
output_data_test_bin = (output_data_test.detach()>0.5).numpy()
tn, fp, fn, tp = confusion_matrix(label_test_tens, output_data_test_bin ).ravel()
A = (tp+tn)/(tp+tn+fn+fp)
P = tp/(tp+fp)
R = tp/(tp+fn)
F1 = 2*(P*R)/(P+R)
print('L\'accuratezza è %0.1f%%' %(A*100))
print('La precisione è %0.1f%%' %(P*100))
print('Il recall è %0.1f%%' %(R*100))
print('Il punteggio F1 è %0.1f%%' %(F1*100))
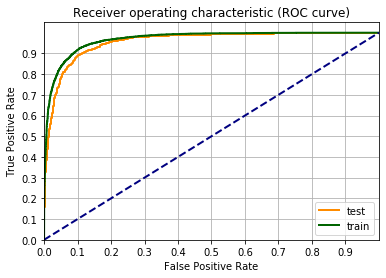
Da 83% a 84.5%, sono quasi al limite delle possibilità. Proviamo un altro step.
lista_pazient_norm_nl = generateNonLinearFeatures(lista_pazienti_norm2.values,5)
label = lista_pazienti_norm.Diabetic.values
lista_pazienti_norm_nl_train, lista_pazienti_norm_nl_test, label_train, label_test = train_test_split(lista_pazient_norm_nl, label, test_size=0.3)
input_data_train_tens = torch.from_numpy(lista_pazienti_norm_nl_train).type(dtype=torch.float)
input_data_test_tens = torch.from_numpy(lista_pazienti_norm_nl_test).type(dtype=torch.float)
label_train_tens = torch.from_numpy(label_train).type(dtype=torch.float).view(-1,1)
label_test_tens = torch.from_numpy(label_test).type(dtype=torch.float).view(-1,1)
model_logreg = nn.Sequential(
nn.Linear(input_data_train_tens.shape[1],1),
nn.Sigmoid()
)
learning_rate = 0.1
optimizer = torch.optim.Adam(model_logreg.parameters(), lr = learning_rate)
for i in range(1000):
output_data_train = model_logreg( input_data_train_tens ) #calcolo l'uscita
loss = error(output_data_train, label_train_tens) #calcolo l'errore
loss.backward() #calcolo del gradiente
optimizer.step() #aggiornamento ei parametri
optimizer.zero_grad() #azzeramento del gradiente
if np.mod(i,100)==0:
print(loss)
output_data_test = model_logreg( input_data_test_tens )
fpr_train, tpr_train, _ = roc_curve(label_train_tens,output_data_train.detach())
fpr_test, tpr_test, _ = roc_curve(label_test_tens ,output_data_test.detach())
fgr1 = plt.figure()
lw = 2
plt.plot(fpr_test, tpr_test, color='darkorange', label="test", lw=lw)
plt.plot(fpr_train, tpr_train, color='darkgreen', label="train", lw=lw)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1])
plt.ylim([0.0, 1.05])
plt.xticks(np.arange(0, 1, 0.1))
plt.yticks(np.arange(0, 1, 0.1))
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic (ROC curve)')
plt.legend(loc="lower right")
plt.grid(which='both')
plt.show()
# output_data_train = model_logreg( input_data_train_tens )
# output_data_train_bin = (output_data_train.detach()>0.5).numpy()
output_data_test_bin = (output_data_test.detach()>0.5).numpy()
tn, fp, fn, tp = confusion_matrix(label_test_tens, output_data_test_bin ).ravel()
A = (tp+tn)/(tp+tn+fn+fp)
P = tp/(tp+fp)
R = tp/(tp+fn)
F1 = 2*(P*R)/(P+R)
print('L\'accuratezza è %0.1f%%' %(A*100))
print('La precisione è %0.1f%%' %(P*100))
print('Il recall è %0.1f%%' %(R*100))
print('Il punteggio F1 è %0.1f%%' %(F1*100))
Il valore di F1 è rimasto intorno al 84%, quindi nessun miglioramento nel passare dalla quarta potenza alla quinta. Inoltre c’è una certa distanza tra la curva riguardante i dati di train e quella di test. Questo indica che c’è un certo overfitting.