Regressione lineare con Pytorch¶
In questo articolo voglio implementare una regressione lineare con Pytorch.
Iniziamo con l'inquadrare il problema.
Ho N variabili di ingresso $x_1,x_2,\dots,x_N$ ed 1 uscita $y$.
Il modello che voglio usare è quello della regressione lineare così definito: \begin{equation*} y = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + … + \theta_N x_N = \Theta \cdot X^T \end{equation*} con: \begin{equation*} \Theta = \begin{bmatrix} \theta_0 & \theta_1 & \dots & \theta_N \end{bmatrix} \end{equation*} \begin{equation*} X = \begin{bmatrix} x_0 & x_1 & \dots & x_N \end{bmatrix} \end{equation*} \begin{equation*} x_0 = 1 \end{equation*}
Quindi devo trovare i parametri $\theta_0,\theta_1,\dots,\theta_N$ tali che l'errore $loss(y_{modello}, y_{target})$ sia il minimo.
Il modello lineare¶
Importiamo i package necessari:
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
Definiamo un modello di regressione lineare con 10 ingressi e 1 uscita, ci serviamo della funzione di PyTorch torch.nn.Linear():
model = nn.Linear(10,1)
i cui parametri sono i pesi (weight) e il bias, in tutto 11 parametri da ottimizzare:
model.weight, model.bias
Definendo un tensore di ingresso con dimensioni 1×10
x = torch.randn(1,10)
l'uscita è data semplicemente da:
y = model(x)
Facciamo un controllo degli shape di ingresso e uscita:
print(x.shape)
print(y.shape)
Otteniamo quanto atteso, un ingresso 1×10 e un'uscita 1×1 (uno scalare).
Ancora una volta voglio verificare che il modelllo di PyTorch faccia quanto atteso, ovvero l'operazione $w \cdot x^T+b$
Definisco un tensore $x$ 1×10 di float
x = torch.tensor([1,23,4,5,6,77,8,9,12,22], dtype=torch.float).view([1,10])
x.shape
L'uscita del modello è:
y1 = model(x)
y1
Verifichiamo che il calcolo $w \cdot x^T+b$ sia giusto. Per fare il prodotto scalare tra i due vettori si usa l'operatore torch.mm
Inoltre occorre che i due tensori di torch.mm siano il primo un vettore riga il secondo un vettore colonna.
Il tensore dei pesi è un tensore riga 1×10:
w = model.weight
w.shape
Poiché x è originariamente un vettore riga 1×10, lo trasformo in un vettore colonna 10×1 usando la funzione .view(). In questo caso x.view(10,1).
Per fare la cosa più generica posso usare x.view(-1,1). Pytorch capisce che è il secondo argomento (1) della funzione che conta e regola il primo di conseguenza.
y2 = torch.mm(w, x.view(-1,1)) + model.bias # w*x+b
y2
Il risultato è quello atteso: y1=y2
Il modello torch.nn.Linear calcola la combinazione lineare degli ingressi come ci attendevamo.
Modello lineare, ingresso singolo e training del modello¶
Facciamo il primo esempio più semplice con un solo ingresso e una sola uscita.
Creiamo un set di dati, costituito da N coppie (x,y), che stanno in una relazione "abbastanza" lineare tra di loro.
Per fare questo definiamo una relazione lineare tra y e x. E aggiungiamo un rumore per rendere la cosa più realistica.
x_samples = torch.linspace(0, 100, steps=101).view(-1,1) #l'ingresso deve essere in formato colonna
m = 13.5 #coefficiente angolare
b = 12 #ordinata all'origine
y_samples_lineare = m * x_samples + b
y_samples_lineare.size()
y_samples_noise = 200 * torch.randn(x_samples.shape[0], 1) #genera un vettore colonna di dati random, con media 0 e varianza 5
y_samples_noise.size()
Abbiamo già visto che i vettori y_samples_lineare e y_samples_noise hanno le stesse dimensioni. Possiamo pertanto sommarli:
y_samples = y_samples_lineare + y_samples_noise
(x_samples, y_samples) è il dataset di punti che devo interpolare (o fittare).
Instanzio il modello lineare con un ingresso e una uscita. Il parametro bias=True indica che devo ottimizare il bias (ordinata all'origine) del modello.
model1 = torch.nn.Linear(1,1, bias=True)
Il modello ha solo due parametri da ottimizzare, che in accordo alla letteratura classica chiameremo $m$ e $q$:
model1.weight, model1.bias
Calcolo le uscite del modello lineare appena definito:
y_linmod = model1(x_samples)
y_linmod.size()
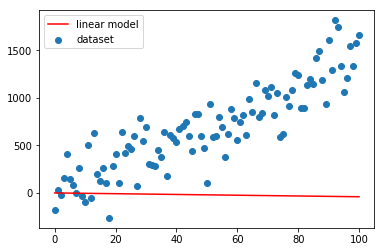
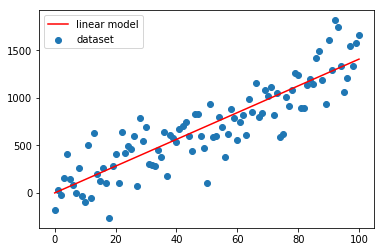
Mettiamo su grafico le due curve (x_samples, y_samples) e (x_samples, y_linmod).
Come si vede il modello lineare non è stato adattato. Pertanto la linea rossa devia nettamente dalla nuvola di punti blu.
plt.scatter(x_samples.numpy(),y_samples.numpy(), label="dataset")
plt.plot(x_samples.numpy(),y_linmod.detach().numpy(),'r', label="linear model")
plt.legend()
plt.show()
Calcolo l'errore quadratico medio tra il dataset e il valore corrente dell'uscita. Per qualche motivo la funzione predefinita di PyTorch nn.MSELoss() mi da errore, pertanto definisco l'errore quadratico medio esplicitamente.
# errore = nn.MSELoss(y_linmod, y_linmod)
errore = torch.mean(torch.pow(y_samples-y_linmod, 2))
errore
Calcolo le derivate parziali dell'errore rispetto ai due parametri m e q, usando la funzione backward().
errore.backward()
Come ottimizzatore uso lo SGD (Stochastic Gradient Descent):
optimizer = torch.optim.SGD(model1.parameters(),1e-4)
Itero su un numero basso di iterazioni, poiché la convergenza è veloce.
for i in range(5):
y_linmod = model1(x_samples)
errore = torch.mean(torch.pow(y_samples-y_linmod, 2))
errore.backward()
optimizer.step()
optimizer.zero_grad()
print(errore)
plt.scatter(x_samples.numpy(),y_samples.numpy(), label="dataset")
plt.plot(x_samples.numpy(),y_linmod.detach().numpy(),'r', label="linear model")
plt.legend()
plt.show()
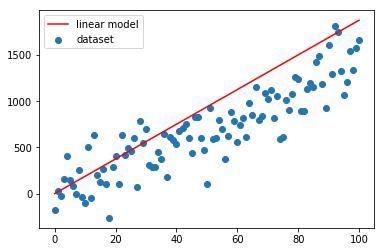
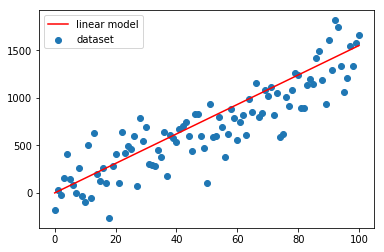
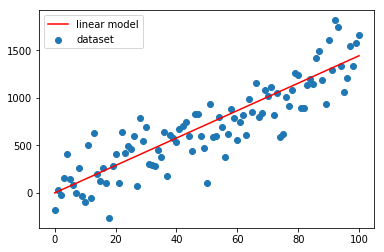
Come si vede dai grafici sopra la convergenza è velocissima, già alla seconda iterazione la linea rossa si attesta sulla nuvola blu.
Un altro paio di iterazioni e il fitting è ottimale.
I parametri ottimizzati sono:
list(model1.parameters())
Come si vede il model.weight è molto vicino al valore di $m = 13.5$ che avevamo usato per generare il dataset.
Il valore di q invece si discosta abbastanza, 12 contro -0.2154
Qualche ipotesi sul perché di questa discrepanza?
Modello di regressione lineare multidimensionale¶
Facciamo un esempio con più variabili di ingresso. 4 ingressi per essere precisi. Questi sono gli step:
- genero un dataset
- creo il modello di regressione lineare
- definisco una funzione errore e un ottimizzatore
- faccio il training del modello
Genero un dataset¶
Creo un dataset di 1000 punti $(x_1,x_2,x_3,x_4,y)$.
Per i dati di ingresso uso la funzione torch.linspace.
I dati di uscita sono una combinazione lineare degli ingressi, i coefficienti $m_i$ sono stati scelti in modo che ogni ingresso contribuisca sull'uscita.
x1 = np.linspace(0,100,50)
x2 = np.linspace(-1,1,50)
x3 = np.linspace(-10,0,50)
x4 = np.linspace(75,150,50)
m1, m2, m3, m4 = 0.5, 25, 50, -0.66 #coeff angolare per ogni direzione
M = torch.tensor([m1,m2,m3,m4]).view([-1,1]) #combino i coeff angolari in un vettore colonna
Genero uno spazio a 4 dimensioni, usando le coordinate x1,x2,x3,x4:
x_comb = np.array([[x1[i],x2[j],x3[l],x4[m]]
for i in range(x1.shape[0])
for j in range(x2.shape[0])
for l in range(x3.shape[0])
for m in range(x4.shape[0])])
x_comb.shape
x_comb
Converto x_comb in un tensore e setto il tipo su flot(=float32), poiché il tipo double(=float64) genera un errore:
X = torch.from_numpy(x_comb).type(torch.float)
Calcolo l'uscita del modello lineare:
y_samples = torch.mm(X,M)
y_samples.shape
Così ho completato la generazione del set di dati (x_samples, y_samples)
Creazione modello Lineare¶
Definiamo il modello:
model2 = torch.nn.Linear(4,1)
Questi sono i parametri, inizializzati in maniera random:
model2.weight, model2.bias
I dati di input li abbiamo definiti in precedenza, verifichiamo il tipo del tensore X:
# X = torch.cat((x1,x2,x3,x4),1)
#X = torch.from_numpy(x_comb).type(torch.float) # setto float altrimenti si setta automaticamente double e da errore
#X.shape
Verifichiamo il tipo dei dati:
X.type()
Calcolo l'uscita del modello lineare, e verifico che lo shape dell'uscita si giusta.
1000 punti di ingresso, ne generano altrettanti in uscita, pertanto è corretto.
y_linmod = model2(X)
y_linmod.shape
L'errore quadratico medio è:
errore = torch.mean(torch.pow(y_samples-y_linmod,2))
errore
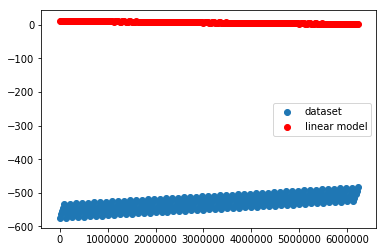
Plottiamo le uscite generate e confrontiamole con quelle del dataset.
Sull'asse x metto l'ordinale del punto.
asse_x = np.linspace(0, X.shape[0]-1, num=X.shape[0])
def downsample_4_plot(asse_x, downsample_factor):
asse_x_dwnsmpl = asse_x[0:-1:downsample_factor]
return asse_x_dwnsmpl
downsample_factor = 25000
asse_x_dwnsmpl = downsample_4_plot(asse_x,downsample_factor)
y_samples_dwnsmpl = downsample_4_plot(y_samples, downsample_factor)
y_linmod_dwnsmpl = downsample_4_plot(y_linmod, downsample_factor)
asse_x_dwnsmpl.shape
y_linmod_dwnsmpl = downsample_4_plot(y_linmod, downsample_factor)
y_linmod_dwnsmpl.shape
asse_x.shape, X.shape, y_samples.shape, y_linmod.shape
asse_x[0:-1:downsample_factor].shape
downsample_factor
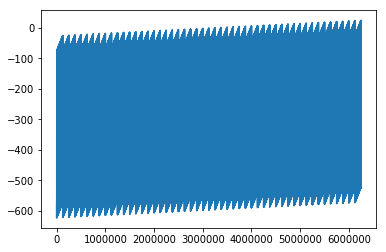
plt.plot(asse_x,y_samples.detach().numpy())
y_samples.numpy()[0:200000:downsample_factor]
y_linmod.detach().numpy()[0:-1:downsample_factor].shape
plt.scatter(asse_x[0:-1:downsample_factor],y_samples.numpy()[0:-1:downsample_factor], label="dataset")
plt.scatter(asse_x[0:-1:downsample_factor],y_linmod.detach().numpy()[0:-1:downsample_factor],c='r', label="linear model")
plt.legend()
plt.show()
Definiamo il SGD come ottimizzatore, indichiamo che i parametri di ottimizzazione sono quelli di model2, e gli diamo un passo di apprendimento abbastanza piccolo da essere sicuri che converga, ma senza essere troppo lenti, dopo qualche iterazione sono arrivato a 5e-5:
model2 = torch.nn.Linear(4,1) #ridefinisco il modello per azzerare i calcoli precedenti
optimizer = torch.optim.SGD(model2.parameters(), 5e-5)
Adesso sono pronto ad eseguire il training del modello.
I passi sono i soliti:
-calcolo dell'uscita
-calcolo dell'errore
-calcolo del gradiente (errore.backward)
-aggionamento dei parametri (optimizer.step)
-reset del gradiente (optimizer.zero_grad)
for itr in range(501):
y_linmod = model2(X) #calcolo l'uscita con il modello corrente
errore = torch.mean(torch.pow(y_samples-y_linmod,2)) #calcolo l'errore tra l'uscita desiderata e l'uscita corrente
errore.backward() #applico la funzione backward, le derivate parziali dell'errore vengono calcolate rispetto alle variabili per cui è definito required_grad=True
optimizer.step() #aggiornamento dei parametri da ottimizzare usando le derivate calcolate nel passo precedente
optimizer.zero_grad() #azzero i gradienti
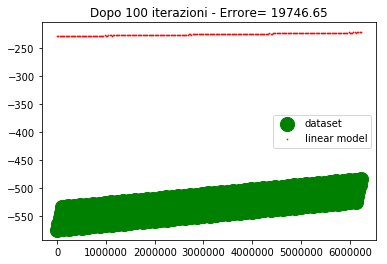
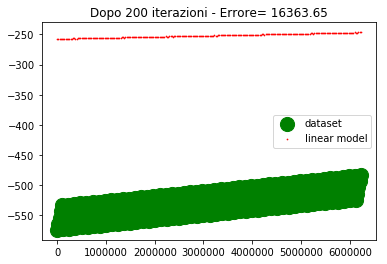
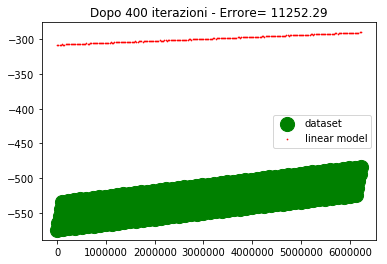
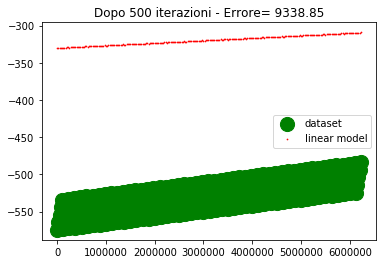
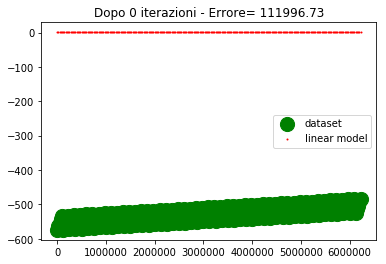
if ((itr==0) or (itr==100) or (itr==200) or (itr==300) or (itr==400) or (itr==500)) : #genera il grafico agli step fissati
plt.scatter(downsample_4_plot(asse_x,downsample_factor),
downsample_4_plot(y_samples, downsample_factor).numpy(),
label="dataset", c='g', s=200)
plt.scatter(downsample_4_plot(asse_x,downsample_factor),
downsample_4_plot(y_linmod, downsample_factor).detach().numpy().reshape(1,-1),
c='r', label="linear model",s=0.5)
plt.legend()
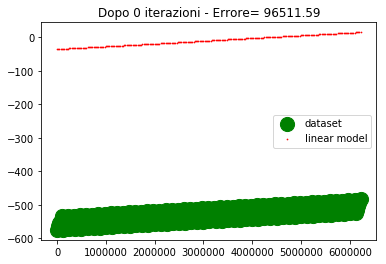
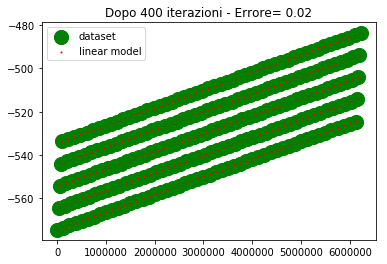
plt.title('Dopo %d iterazioni - Errore= %1.2f' %(itr,errore))
plt.show()
Come si vede dopo 500 iterazioni l'errore è abbastanza alto e la convergenza abbastanza lenta.
Se provo ad alzare il learning rate, l'errore inizia a divergere, per cui non è una strada praticabile.
La domanda che mi pongo è: come mai con un learning rate così basso (5e-5) la convergenza è così critica che basta alzare il learning rate di poco (per esempio 1e-4) perché la convergenga sia compromessa.
La risposta che riesco a darmi è che gli ordini di grandezza delle variabili d'ingresso sono diversi, per cui lo spostamento del punto (dipendente dal learning rate e dal gradiente) deve essere compatibile con tutte le variabili, pertanto deve essere piccolo.
Vediamo se riesco a velocizzare la convergenza normalizzando le variabili $x_1, x_2, x_3, x_4$.
Normalizziamo le coordinate.
m = X.min(dim=0) #valore minimo per ogni colonna di X
M = X.max(dim=0) #valore massimo per ogni colonna
u = (M.values+m.values)/2 #valor medio per ogni colonna
d = (M.values-m.values).view([1,-1]) #intervallo min-max, per ogni colonna
Ad ogni coordinata sottraggo il suo valor medio e divido per l'intervallo di variazione: \begin{equation*} \hat{x_i} = \frac {x_i – u}{d} \hspace{1cm} \forall i=1,2,3,4 \end{equation*}
Il nuovo set di coordinate è $\hat{x_1},\hat{x_2},\hat{x_3},\hat{x_4}$.
Per fare questo calcolo uso torch.mul che realizza una moltiplicazione elemento-per-elemento tra i due operatori. Es.:
\begin{equation} \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{bmatrix} \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} \begin{bmatrix} a_{11}*b_1 & a_{12}*b_2 \\ a_{21}*b_1 & a_{22}*b_2 \\ a_{31}*b_1 & a_{32}*b_2 \end{bmatrix} \end{equation}
X_norm = torch.mul((X-u),1/d)
Azzero il modello e ridefinisco l'ottimizzatore con un learning rate di 0.1
model2 = torch.nn.Linear(4,1) #ridefinisco il modello per azzerare i calcoli precedenti
optimizer = torch.optim.SGD(model2.parameters(), 0.1)
Copio il codice di prima per fare il training del modello, cambio solo l'ingresso, stavolta userò X_norm invece di X.
for itr in range(501):
y_linmod = model2(X_norm) #calcolo l'uscita con il modello corrente
errore = torch.mean(torch.pow(y_samples-y_linmod,2)) #calcolo l'errore tra l'uscita desiderata e l'uscita corrente
errore.backward() #applico la funzione backward, le derivate parziali dell'errore vengono calcolate rispetto alle variabili per cui è definito required_grad=True
optimizer.step() #aggiornamento dei parametri da ottimizzare usando le derivate calcolate nel passo precedente
optimizer.zero_grad() #azzero i gradienti
if ((itr==0) or (itr==100) or (itr==200) or (itr==300) or (itr==400) or (itr==500)) : #genera il grafico agli step fissati
plt.scatter(downsample_4_plot(asse_x,downsample_factor),
downsample_4_plot(y_samples, downsample_factor).numpy(),
label="dataset", c='g', s=200)
plt.scatter(downsample_4_plot(asse_x,downsample_factor),
downsample_4_plot(y_linmod, downsample_factor).detach().numpy().reshape(1,-1),
c='r', label="linear model",s=1)
plt.legend()
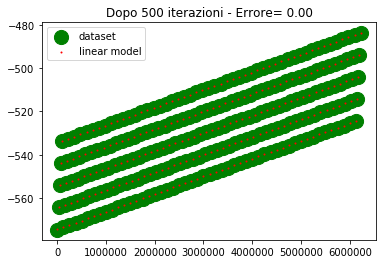
plt.title('Dopo %d iterazioni - Errore= %1.2f' %(itr,errore))
plt.show()
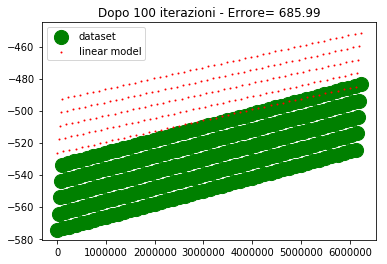
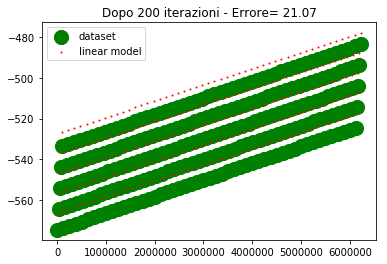
Sull'asse y abbiamo i valori di uscita, sull'asse x abbiamo l'ordinale del punto (e non la variabile di ingresso, poichè era impossibile riprodurre i 4 ingressi su grafico).
Per come sono fatti i dati, 4 assi ridotti ad un ordinale, sembra che ci siano 5 linee diverse in realta è un artefatto, dovuto al fatto che mi sto ostinando a rappresentare una cosa che non dovrei.
I valori desiderati li ho rappresentati con un marker molto spesso in modo che la posizione relativa tra le due curve sia ben visibile specialmente nel caso in cui sono vicine o sovrapposte.
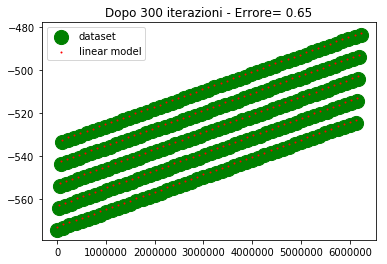
Come si vede alla 300esima iterazione i due modelli lineare iniziano a sovrapporsi. Alla 500esima iterazione sono praticamente sovrapposti e l'errore è nullo (o molto basso).
Il training ci ha consegnato questi valori dei parametri ottimizzati:
model2.weight, model2.bias
I coefficienti angolari così ottenuti devono essere denormalizzati per tornare allo spazio $\mathbb{R}^4$ originale.
Per farlo divido ciascuna coordinata per il delta $d$ che avevo calcolato qualche step sopra.
Anche in questo caso faccio una moltiplicazione elemento-per-elemento con torch.mul
torch.mul(model2.weight,1/d)
Facciamo un confronto con i valori usati per generare il dataset:
m1 = 0.5 vs 0.4999
m2 = 25 vs 24.9961
m3 = 50 vs 49.9919
m4 = -0.66 vs -0.6599
Come si vede i valori trovati sono praticamente perfetti
Usando i parametri ottimizzati calcolo l'uscita e l'errore:
y_linmod = model2(X_norm)
errore = torch.mean(torch.pow(y_samples-y_linmod,2))
errore
Come atteso l'errore è molto basso.